Beton a żelbet
Problem z obliczeniami termicznymi w postaci modeli numerycznych 2D i 3D polega na tym, że dają wyniki ściśle odpowiadające wprowadzonym danym. Innymi słowy, są podatne na błędy merytoryczne i logiczne operatora programu. Operator zaś opiera się na dostępnych mu danych. Są to zwykle źródła normowe, podręczniki, atesty etc.
Szukając danych o współczynniku przewodzenia ciepła „λ” dla żelbetu, możecie Państwo znaleźć dane jak poniżej. Jest to wyciąg z przedruku normy z 1999r. Podobnie podawała jeszcze starsza norma tj. 1984r. Przeglądając Internet nie mogłem znaleźć innych danych.
Rys. 1. Dane dla betonu i żelbetu znalezione w Internecie.
| Nazwa materiału | Gęstość w stanie suchym (średnia) Kg/m3 | Współczynnik przewodzenia ciepła λ [w/mK] | |
| Warunki średniowilgotne | Warunki wilgotne |
||
| Beton zwykły, żelbet | 2500 | 1,70 | 1,80 |
Beton jest materiałem w miarę jednorodnym i można przyjąć, że przy danej gęstości i rodzaju kruszywa, będzie on miał ten sam współczynnik przewodzenia ciepła w każdym kierunku i dla każdej próbki. Podawanie dla niego parametru w powyższej tabelce nie jest błędem.
Dopiero norma PN-EN 12524 wprowadza rozróżnienie pomiędzy betonami a żelbetami i podaje wartości współczynnika przewodzenia ciepła dla (na podstawie tab. 1 str. 4 PN-EN 12524):
betonu zbrojonego w stopniu 1% 2,3W/(mK)
betonu zbrojonego w stopniu 2% 2,5W/(mK).
Żelbet jest to konglomerat szkieletu stalowego i wypełniacza betonowego. Skoro więc beton użyty w żelbecie wykazuje się wartością np. λ=1,70 W/(mK), stal λ=50,00 W/(mK), współczynnik przewodzenia ciepła zastępczy, będzie wynikiem współpracy obu materiałów i ich ilościowej proporcji a także otulenia zbrojenia.
W celu przedstawienia zależności współczynnika „λ” od kierunku przepływu ciepła oraz ilości zbrojenia przeprowadziliśmy szereg obliczeń 3D (trójwymiarowych) wycinków żelbetowych płyt oraz słupa. Wyniki potwierdziły przypuszczenia, że wartość współczynnika przewodzenia ciepła rośnie wraz z ilością zbrojenia (stopniem zbrojenia).
Obliczenia wykonano przy założeniach:
– współczynnik przewodzenia ciepła betonu λ=1,70 W/(mK);
– współczynnik przewodzenia ciepła stali zbrojeniowej λ=50,00 W/(mK);
– otulenie zbrojenia 30mm
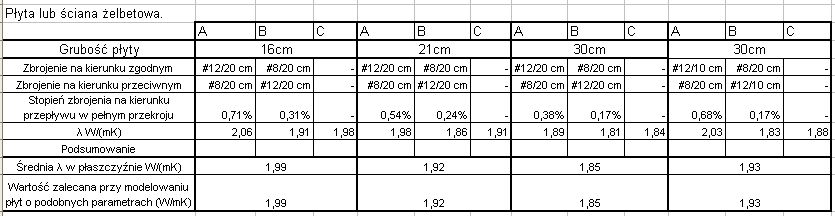
Tab.1.
A – kolumna dla kierunku zgodnego ze zbrojeniem głównym;
B – kolumna dla kierunku zbrojenia rozdzielczego;
C – kolumna dla kierunku prostopadłego do płaszczyzny przegrody.
Można się pokusić o stworzenie prostej recepty na obliczanie współczynnika przewodzenia ciepła i sprawdzenie, czy ta recepta będzie zgodna z powyższymi wynikami.
Mamy warunki podstawowe:
dla μ=0,0% λ=1,70 W/(mK);
dla μ=100,0% λ=50,00 W/(mK);
Zakładamy przebieg prostoliniowy (nie twierdząc, że jest właściwy).
λ’=1,7+(50-1,7)/100* μ = 1,7+0,483 * μ [1]
Co daje dla
0,71% λ’=2,04 podczas, gdy wiemy że λ=2,06 błąd 1,0%
0,31% λ’=1,85 podczas, gdy wiemy że λ=1,91 błąd 3,1%
dla wartości średniej
0,51% λ’=1,95 podczas, gdy wiemy że λ=1,99 błąd 2,0%
0,54% λ’=1,96 podczas, gdy wiemy że λ=1,98 błąd 1,0%
0,24% λ’=1,82 podczas, gdy wiemy że λ=1,86 błąd 2,2%
dla wartości średniej
0,39% λ’=1,89 podczas, gdy wiemy że λ=1,92 błąd 1,6%
0,68% λ’=2,03 podczas, gdy wiemy że λ=2,03 błąd 0,0%
0,17% λ’=1,78 podczas, gdy wiemy że λ=1,83 błąd 2,7%
dla wartości średniej
0,43% λ’=1,91 podczas, gdy wiemy że λ=1,93 błąd 1,0%
Podstawmy do tej zależności wartości z PN-EN 12524.
1,00% λ’=2,18 podczas, gdy wg. normy λ=2,30 błąd 5,2%
2,00% λ’=2,66 podczas, gdy wg. normy λ=2,50 błąd 6,4%
Wszystkie powstałe w ten sposób błędy są mniejsze niż zastosowanie dla żelbetu parametru jak dla betonu. Dlaczego jednak różnica powiększa się w stosunku do wielkości normowej. Dlatego, że przyjęto uśrednienie dla jakiegoś przedziału zbrojenia i dla różnych gęstości samego betonu. Pragnę zauważyć, że w tabeli podano:
beton zbrojony 1% stali o gęstości 2300kg/m3
beton zbrojony 2% stali o gęstości 2400kg/m3.
Nie wiadomo dokładnie o jakiej gęstości mowa – samego betonu współpracującego ze stalą, czy betonu i stali łącznie. Należy zakładać, że samego betonu, gdyż żelbet nie może mieć mniejszej gęstości niż beton niezbrojony.
Dodatkowo my operujemy tylko elementami płytowymi o określonym otuleniu i zbrojeniu dwukierunkowym. Słupy będą wykazywały inne właściwości ze względu na inny charakter zbrojenia. Norma odnosi się do wszystkich konstrukcji żelbetowych nie wdając się w szczegóły. Jest to bardzo duże uśrednienie.
Uczulamy, że przewodność cieplna żelbetu może być o wiele większa niż betonu, co zostało udowodnione. Gdy rozpatrujemy prosty przypadek ściany bez mostków cieplnych (poza samym zbrojeniem, które stanowi wewnętrzne mostki cieplne żelbetu w stosunku do betonu), ma to dużo mniejsze znaczenie, gdyż w każdym przypadku ściany czy stropu, przegroda warstwowa (z ociepleniem) będzie bardziej swą oporność zawdzięczała ociepleniu niż warstwie żelbetu. Czasami można nawet pominąć opór cieplny stropu, czy ściany żelbetowej w obliczeniach oporu łącznego.
Działa to na korzyść parametrów nowoprojektowanego budynku, chociaż trochę przekłamuje wynik. Gdy jednak liczymy modele 2D lub 3D z mostkami cieplnymi żelbetowymi lub innej natury z udziałem konstrukcji żelbetowej, pominięcie wpływu zbrojenia na przewodność cieplną żelbetu prowadzi do znacznych błędów. W takich przypadkach należy przyjmować normowe wartości współczynnika przewodzenia ciepła żelbetu lub na bazie konkretnego zbrojenia i jego ułożenia zbudować precyzyjne modele 3D uwzględniające zbrojenie. Niestety ta druga metoda jest bardzo czasochłonna oraz potrzebuje dużo pamięci operacyjnej komputera.
Norma uśrednia współczynnik przewodzenia ciepła na wszystkie kierunki. W przypadku ekspertyz, często konieczne jest określenie przyczyn przemarzania w danym miejscu, w okolicach belek, nadproży, słupów czy belek obwodowych. W takich przypadkach ważne jest by określić właściwe parametry na poszczególnych kierunkach przewodzenia ciepła.
Zalecam interpolację wartości normowych (np. wzorem podobnym do [1] chociaż nie będą to wartości ściśle prawdziwe, lub liniowo pomiędzy dwoma podanymi przez normę stopniami zbrojenia), gdyż norma nie daje nam żadnych innych narzędzi.
W przypadku stropów i ścian przez nas przeanalizowanych, można wyciągnąć wnioski, że średnia wartość „λ” obu kierunków w płaszczyźnie jest bliska wartości „λ” w kierunku prostopadłym do płaszczyzny. Dlatego nie popełni się wielkiego błędu przyjmując wartość średnią – normową jako wartość obowiązującą na wszystkich trzech kierunkach w modelach 3D.